Разделы
Счетчики
Структура семантической нейронной сети, реализующей морфологический и синтаксический разбор текста
Процесс обработки текста на естественном языке можно разбить на несколько уровней: разбор, анализ и синтез. Уровень разбора определим как функцию преобразования текста на естественном языке из неформализованного вида в формализованное внутреннее представление. Уровень анализа - функция преобразования данных, существующих во внутреннем представлении и вывода на их основе новых данных, так же в формализованном виде. Уровень синтеза - функция формирования ответа на естественном языке, адекватного внутреннему формализованному представлению.
Уровень разбора можно разделить на несколько последовательных операций: морфологический, синтаксический и семантический разбор. Морфологический разбор проводится путем выделения из текста отдельных слов и разбором выделенных слов на морфемы. Операция синтаксического разбора текста естественного языка представляет собой определение всех синтаксических признаков и синтаксических связей этих слов, необходимых для семантического разбора [1, стр. 34]. Семантический разбор требует наличия в памяти системы имитационной модели внешнего мира. Он заключается в окончательном формировании внутреннего формализованного представления текста путем сопоставления фактов, находящихся непосредственно в тексте с знаниями из имитационной модели [1, стр. 51, 2 стр. 188].
Рассмотрим операции морфологического и синтаксического разбора текста естественного языка. Выделение отдельных слов из текста в электронном виде не представляет трудности, так как в этом случае слова отделяются специальным символом "пробел". Для Русского языка задача морфологического и синтаксического разбора может быть решена с помощью данных содержащихся в грамматическом словаре Русского языка [3]. В нем приводятся информация о словообразовании, словоизменении и определении синтаксических признаков отдельных слов.
Реализация уровня разбора текста требует наличия некоторой формальной модели этого разбора. Согласно теореме Гёделя реализация формализма может оказаться проще описания этого формализма. Упоминая теорему Гёделя, фон Нейман пишет: "… В таком случае быстрее сделать что-то, чем описать, быстрее привести схему, чем дать общее описание всех ее функций и всех мыслимых обстоятельств. Очень важно понять, что сеть из формальных нейронов может сделать все, что можно описать словами, и это необычайно упрощает дело при низких уровнях сложности. Но при высоких уровнях сложности это не обязательно будет упрощением. Вполне возможно, что при высоких уровнях сложности ценность представляет собой обратное утверждение этой теоремы [Гёделя], т. е. она упрощает дело потому, что гарантирует обратное: можно выразить логику на языке этих построений [формальных нейронов], а прямое утверждение может быть и неверным"[4, стр. 67].
Из этого утверждения Неймана следует, что, возможно, в качестве формального представления следует брать не формальные математические модели, а реализацию этих моделей. Одним из вариантов такого формального представления может выступать формальная нейронная сеть. Поэтому можно попытаться воспользоваться формальной нейронной сетью для решения задач морфологического и семантического разбора текста, а так же задачи словоизменения.
В работе [4] описано функционирование формальной нейронной сети Маккаллока-Питтса. Отдельные нейроны в нейронной сети Маккаллока-Питтса представляют собой логические операции и, или и не. В зависимости от результата выполнения логической операции, нейрон имеет состояния возбуждения или покоя, соответствующие логическим значениям истина и ложь. "… Временная задержка, связанная с работой каждого нейрона, гарантирует эффективный и конструктивный характер получаемой здесь логической системы" [4, стр. 118]. Поскольку число нейронов в сети конечно и число состояний у нейрона конечно, такая нейронная сеть является автоматом с конечным числом состояний. Нейрон в сети Маккаллока-Питтса может находиться только в двух логических состояниях и обеспечивает выполнение только функций алгебры-логики. Естественный язык оперирует с нечеткими и неполными понятиями. Поэтому нейронная сеть Маккаллока-Питтса без дополнительных усилий не обеспечивает обработку нечетких понятий текста естественного языка.
Для решения задач морфологического и синтаксического анализа текста, а так же задач анализа словоизменения применим семантическую нейронную сеть[5], близкую по свойствам формальной нейронной сети Маккаллока-Питтса. Отличие семантической нейронной сети от сети Маккаллока-Питтса заключается в том, что в сети Маккаллока-Питтса выполняются логические операции Булевой алгебры, а в семантической нейронной сети операции нечеткой логики [5]. В нечеткой логике для определения степени истинности утверждения используется фактор уверенности - число находящееся в некотором интервале, например от 0 до 1. Максимальное значение из этого интервала обычно интерпретируется как полная уверенность в возникновении события, а минимальное значение - как полная уверенность в его отсутствии.
В отличие от теории вероятности фактор уверенности выражает субъективную уверенность в возникновении события и не имеет никакого статистического смысла [6 стр. 196]. Нейроны в семантической нейронной сети соответствуют элементарным понятиям естественного языка и обрабатывают дискретные градиентные значения. Каждый нейрон этой сети имеет конечное число состояний. Следовательно, семантическая нейронная сеть может рассматриваться как конечный автомат.
В качестве структуры семантической нейронной сети, выполняющей морфологический и синтаксический разбор, выберем синхронизированное линейное дерево [7]. Проведем грубую оценку объема нейронной сети, требуемой для реализации грамматического словаря Русского языка. В словаре А.А. Зализняка содержится около 100000 словарных статей. Допустим, каждая словарная статья содержит в себе 10 слов по 10 символов. Тогда Общее количество неупакованной информации составит 10*10*100000 = 107 символов. В семантической нейронной сети каждый символ соответствует отдельному нейрону.
Пусть, в среднем, каждый нейрон занимает в хранилище [8] 1000 байт. Тогда общий объем хранилища для семантической нейронной сети, реализующей грамматический словарь А.А. Зализняка, составит 1010 байт или около 10 гигабайт. Накопители такого объема уже давно не являются экзотикой, следовательно, имеется возможность полностью представить грамматический словарь в виде семантической сети, в которой каждой форме слова из словарной статьи будет соответствовать отдельное слово в виде фрагмента нейронной сети. На практике, грамматический словарь, реализованный в виде семантической нейронной сети, будет иметь меньший объем. Это связанно с тем, что в синхронизированном линейном дереве, используемом для хранения словоформ, одинаковые символьные последовательности разных слов хранятся как один фрагмент линейного дерева.
Слой извлечения смысла в виде синхронизированного линейного дерева можно рассматривать как конечный автомат, так как число нейронов в сети ограниченно, и они имеют конечное число состояний и связей. Переход из одного состояния в другое происходит при подаче на слой извлечения смысла очередного символа входной последовательности. Удобно рассматривать слой извлечения не как один автомат, а как несколько конечных субавтоматов - по числу словарных статьей. Удобно также считать, что один нейрон имеет одно градиентное субсостояние в диапазоне от покоя до возбуждения. Пусть каждое такое субсостояние - элементарный смысл. Можно сказать, что одному активному субсостоянию нейроавтомата соответствует один или несколько возбужденных нейронов. Тогда в одном фрагменте синхронизированного линейного дерева (в одном автомате) мы получим несколько субавтоматов - по числу словарных статей или несколько состояний у одного автомата одновременно. Это решение позволит в дальнейшем справится с многозначностью естественного языка. Рассмотрим модель нейрона словарной статьи. Реализация семантической нейронной сети на последовательной вычислительной системе предъявляет к быстродействию нейронов дополнительные требования. Следует, по возможности, увеличить скорость работы отдельного нейрона и уменьшить количество нейронов в сети, так как в этом случае нейроны обрабатываются последовательно, один за другим, и поэтому общее время расчета одного такта системы равно количеству обрабатываемых нейронов умноженное на время обработки одного нейрона. Для уменьшения количества нейронов и увеличения скорости их работы объединим дизъюнктор и конъюнктор в одном нейроне (рис.1).
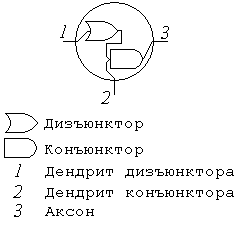
Рис. 1
При этом у каждого нейрона будет по два дендритных дерева: одно - выполняющее функцию дизъюнкции входных градиентных значений, другое - выполняющее функцию конъюнкции входных градиентных значений и результата функции дизъюнкции. Нейрон обозначим кругом, его дендрит дизъюнктора обозначим слева от этого круга (рис.1, п.1) , дендрит конъюнктора сверху или снизу от круга (рис.1, п.2), аксон - справа от круга (рис.1, п.3). Для удобства внутри круга будем записывать символы, соответствующие дендриту конъюнктора.
Рассмотрим модель словарной статьи. Отдельная словарная статья представляет собой главное слово, несущее основную смысловую нагрузку статьи, и группу словоформ, получающуюся из главного слова путем словоизменения (спряжения или склонения). Пусть одна словарная статья - это группа нейронов, или один нейронный субавтомат в слое извлечения смысла. Пусть общее число субсостояний словарной статьи равно числу словоформ этой статьи. Пусть каждое субсостояние такого субавтомата представляет собой один возбужденный нейрон. При этом, в случае одновременного возбуждения двух разных нейронов одного субавтомата будем говорить что субавтомат имеет одновременно два разных субсостояния. Каждая словарная статья имеет главный нейрон, соответствующий этой статье. Главный нейрон словарной статьи возбужден всегда, когда распознано слово, принадлежащее его словарной статье. Каждой словоформе соответствует отдельный нейрон. Он возбуждается в случае, если словоформа распознана.
В слое извлечения смысла существуют нейроны, не принадлежащие отдельным словарным статьям. Эти нейроны соответствуют признакам словоформ общим для многих словарных статей, таким как род, падеж, число, время ... Они возбуждаются при возбуждении словоформ, обладающих соответствующими признаками. Будем считать, что состояния этих нейронов, соответствующие признакам словоформ, так же принадлежат к субавтоматам словарных статей, с которыми эти нейроны образуют связи. Тогда, несколько словарных статей могут одновременно находиться в одном и том же состоянии. Например, все словарные статьи, распознающие слово "коса" будут одновременно находиться в состоянии "существительное", или, что тоже самое, общий нейрон, соответствующий признаку "существительное" будет находиться в возбужденном состоянии.
Множество возбужденных нейронов субавтомата соответствует множеству признаков, принадлежащих отдельной словоформе, распознанной субавтоматом. Задача классификации или определения словарной статьи и словоформы по заданной символьной последовательности сводится к прохождению волны возбуждения через слой извлечения смысла и возбуждению соответствующего субавтомата для соответствующей словарной статьи. Задача словоизменения сводится к изменению состояния такого субавтомата из начального состояния - соответствующего словоформе из которой начинается словоизменение в конечное состояние - соответствующее словоформе в которую требуется преобразовать исходную словоформу.
Рассмотрим структуру связей нейронной сети, обеспечивающую решение описанных задач. Синхронизированное линейное дерево обеспечивает решение задачи классификации словоформы по словарным статьям и определение признаков этой словоформы. В случае наличия многозначности, в синхронизированном линейном дереве возбуждаются все словарные статьи и словоформы, соответствующие всем отдельным значением словоформы. Например, при подаче на вход синхронизированного линейного дерева [7] слова "косе" будут возбуждены словарные статьи, соответствующие значениям "коса-волосы", "коса-инструмент", "коса-ландшафт". При этом в каждой словарной статье будут возбуждены по две словоформы, соответствующие дательному и предложному падежам.
Для решения задач словоизменения/словообразования так же можно использовать синхронизированное линейное дерево. В этом случае оно будет выступать как переключательная цепь, коммутирующая возбуждение, переводящее субавтомат из одного состояния в другое. Переключение состояний субавтомата будет происходить при подаче на вход синхронизированного линейного дерева специальных команд. Эти команды будут распознаны синхронизированным линейным деревом и преобразованы в градиентное значение на выходе соответствующих им нейронов-эффекторов, что вызовет возбуждение или торможение нейронов, соответствующих состояниям словарной статьи.
Опишем внутреннюю структуру словоформы в синхронизированном линейном дереве. Непечатный символ пробела между словами будем обозначать "_". Для удобства отделения словоформ от служебных символьных последовательностей примем решение начинать каждое слово со спецсимвола, не имеющего аналога в символах находящихся в обрабатываемой символьной последовательности. Для удобства работы ограничим множество символов внешнего мира множеством букв и цифр русского языка. В качестве "старт" спецсимвола словоформы применим символ точки: ".". Рецептор спецсимвола "." возбуждается пробелом "_", находящимся перед первым непробельным символом словоформы. Каждую словоформу во входной последовательности так же завершает пробельный символ "_". Введем два разных равноправных рецептора - "%" и "$" реагирующие на символ пробела и на спецсимволы "%" и "$" соответственно. Первый рецептор будем использовать в качестве детектора конца словоформы как единицы словарной статьи (слово обыкновенное), а второй - как детектор признака словоформы (падеж, число, спряжение, …) так же совпадающий с концом словоформы. Фрагмент синхронизированного линейного дерева построенный для слов ".коса_" и ".косе_" изображен на рис.2.
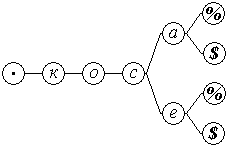
Рис. 2
Синхронизированное линейное дерево, изображенное на рис.2 переходит в состояние "." при подаче на его вход спецсимвола ".", потом - в состояние ".к" при подаче символа "к", далее последовательно ".ко", ".кос", ".косе", и затем одновременно два субсостояния ".косе%" и ".косе$", при подаче соответственно "о", "с", "е", "_".
Рассмотрим признаки словоформ. Символом "*" обозначим первый спецсимвол признака словоформы, выступающий в той же роли, что и символ "." для словоформ. Начало словоформы и ее признака обозначаем различными спецсимволами для уменьшения размера дерева поиска, это может увеличить скорость работы последовательной вычислительной системы. Однако, для решения задачи словоизменения на параллельной вычислительной системе, было бы достаточно ограничиться различением спецсимволов "$" и "%". На рис.3 приведен пример структуры связей словарной статьи, определяющей следующие признаки: существительное -"*сущ$" именительный -"*имн$" и дательный -"*дат$" падежи слов ".коса_" и ".косе_". При подаче на словарную статью слова ".коса_" она переходит в возбужденные субсостояния: ".коса%", "*сущ$", "*имн$", а при подаче слова ".косе_" в возбужденные субсостояния: ".косе%", "*сущ$" и "*дат$".
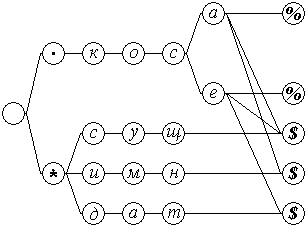
Рис. 3
Введем операцию принудительного связывания, обозначаемую спецсимволом "-". Эта операция будет связывать два нейрона, имеющие возбужденное состояние, после подачи на вход синхронизированного линейного дерева двух фрагментов символьных последовательностей расположенных слева и справа этого символа. При этом возбужденный нейрон левой части выражения образует аксон, а возбужденный нейрон правой части выражения - дендрит. Задание на компиляцию фрагмента сети с рис.3 приведено на рис.4.
.коса% .косе% .коса-*сущ$ .косе-*сущ$ .коса-*имн$ .косе-*дат$ |
Нейроны рецепторы распознают отдельные символы входной символьной последовательности. На выходе рецептор генерирует сигнал, означающий наличие или отсутствие соответствующего символа в анализируемом тексте. Нейроны-эффекторы выдают результат распознавания отдельных фрагментов входной символьной последовательности. Заменив в синхронизированном линейном дереве сигнал от рецептора сигналом от эффектора того же дерева, получим возможность использовать в качестве входных символов фрагменты символьных последовательностей.
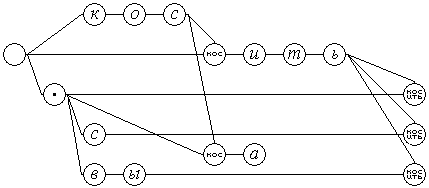
Рис. 5
Для обозначения таких фрагментов во входной символьной последовательности будем применять спецсимволы скобок: "(" и ")". Задание на компиляцию слоя извлечения смысла, изображенного на рис.5 приведено на рис.6.
.(кос)а .((кос)ить) .с((кос)ить) .вы((кос)ить) |
Задача разбора свелась к прохождению волны возбуждения по слоям синхронизированного линейного дерева. Результат разбора представляется в виде совокупности субсостояний этого дерева. Задача словоизменения сводится к изменению состояния субавтомата - словарной статьи из состояния склоняемой словоформы в состояние результата склонения. Для обеспечения этой функциональности необходимо ввести связи для перехода между состояниями словарной статьи. Следует заметить, что в случае словоизменения, изменяемое слово уже имеется в наличии и уже обработано словарной статьей. Поэтому начальным состоянием для задачи словоизменения является одно из возбужденных состояний словарной статьи. Переход из одного возбужденного состояния соответствующего начальной форме слова в конечное состояние, соответствующее конечной форме слова происходит при подаче на линейное синхронизированное дерево соответствующего спецсимвола.
В качестве спецсимволов, служащих для перевода словарных статей из одного состояния в другие выберем не один символ, а целую символьную последовательность. Это возможно благодаря тому, что как упоминалось ранее, любой нейрон можно рассматривать и как эффектор и как рецептор. Некоторая символьная последовательность, поданная на вход синхронизированного линейного дерева, в случае успешного распознавания, возбуждает один или несколько нейронов этой сети. Сигнал с этого возбужденного нейрона можно использовать в качестве выходного сигнала рецептора. Связь, обеспечивающая перевод словарной статьи из одного субсостояния в другое будет представлять нейрон, выполняющий функцию конъюнкции с двумя входами, один - с нейрона представляющего субсостояние, с которого требуется провести переход, другой - сигнал с рецептора, распознающего спецсимвол перевода, а выход - возбуждающий нейрон, представляющий субсостояние, в которое требуется перейти по приходу спецсимвола.
На рис.7 приведен пример задания на программирование словоизменения слов "коса-косе" и "косе-коса" в сети рис.3. На рис.8 приведена структура нейронной сети, образованная после выполнения этого задания. При подаче на данную структуру символьной последовательности ".коса_(*дат$)_" возбуждаются состояния ".косе%", "*сущ$", "*дат$", те же что и при подаче символьной последовательности ".косе_". Если подать на эту структуру символьную последовательность ".косе_(*имн$)_", то возбуждаются состояния ".коса%", "*сущ$", "*имн$", те же что и при подаче последовательности ".коса_".
.коса%(*дат$)-.косе_; .косе%(*имн$)-.коса_; |
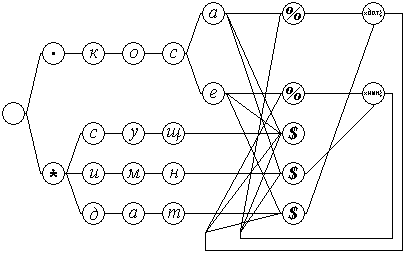
Рис. 8
Спецсимвол "&" применяется для обозначения одновременного возбуждения нескольких нейронов. Каждая из нескольких символьных последовательностей, поданных одна за другой на вход синхронизированного линейного дерева, последовательно возбуждает собственные наборы нейронов. Запись этих последовательностей через знак "&" обозначает одновременное объединение возбужденных ими нейронов в один набор.
В качестве программирующей последовательности спецсимвол "&" приводит к созданию нейрона, выполняющего конъюнкцию выходных сигналов всех нейронов объединенных в этот набор. Так происходит в связи с тем, что аксоны объединенных в набор возбужденных нейронов связываются с дендритом обучаемого нейрона, который выполняет конъюнкцию всех поступающих на него сигналов. Следовательно, этот нейрон будет возбужден только в случае одновременного возбуждения всех нейронов входящих в описанное объединение.
На рис.9 приведено задание на программирование фрагмента нейронной сети, распознающей последовательность из существительного множественного числа и глагола множественного числа. На рис.10 показана структура связей синхронизированного линейного дерева, полученная после запуска этого задания. Условно изображенный на рисунке эффектор "1" будет возбуждаться при поступлении символьных последовательностей, таких как "машины едут" или "спортсмены бегут" и будет находиться в покое при поступлении "машина едет" или "спортсмены бежит".
(*сущ$ & *мно$)(*гла$ & *мно$) |
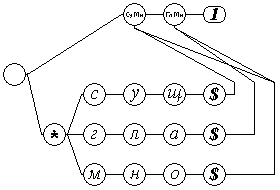
Рис. 10
Программирование (обучение) синхронизированного линейного дерева проводится по принципу запоминания всей новой информации, поступившей на его вход. Новой считается та информация, которая на момент поступления отсутствует в программируемой нейронной сети. В режиме программирования на каждом такте работы обучаемой нейронной сети производится поиск возбужденных нейронов. Если возбужденные нейроны были найдены, то считается, что сеть уже успешно извлекла смысл из предложенной символьной последовательности и обучение проводить не нужно. В случае если возбужденных нейронов не было найдено, в сети создаются новые нейроны с таким условием, чтобы они были бы возбуждены в случае прихода программирующей последовательности. Все созданные нейроны переводятся в возбужденное состояние. Таким образом, после проведения такта программирования сеть находится в таком состоянии, как будто программирования не проводилось, а сеть была уже заранее обучена, и успешно обработала входную символьную последовательность.
Предложенная структура семантической нейронной сети в состоянии выполнять операции морфологического и синтаксического разбора и операцию словоизменения с некоторыми ограничениями. Она не в может правильно обрабатывать морфологический разбор и словообразование слов с приставками без дополнительной помощи в виде выделения этих приставок спецсимволами "()". Этот недостаток можно обойти, рассматривая слово без приставки и слово образованное добавлением приставки как два разных слова и понятия, а не две формы одного. Линейное дерево не позволяет обрабатывать рекурсивные отношения между словами, когда в качестве элемента некоторого отношения выступает само это отношение или другое отношение имеющее первое в своем составе.
Этот недостаток приводит к чрезмерному расходу нейронов и необходимости программировать семантическую нейронную сеть с учетом наиболее возможно глубокого рекурсивного отношения, преобразовывая его при программировании в последовательность не рекурсивных отношений. Таким образом, предложенная структура сети в состоянии извлекать из символьной последовательности некоторое, определяемое структурой сети, подмножество проективных связей. Возможность обработки любых проективных связей семантической нейронной сетью требует дальнейшего исследования.
Литература
- Виноград Т. Программа, понимающая естественный язык. - М.: "Мир", 1976. - 296 с.
- Поспелов Д.А. Фантазия или наука: на пути к искусственному интеллекту - М.: Наука. Главная редакция физико-математической литературы, 1982.-224 с.
- Зализняк А.А. Грамматический словарь русского языка: Словоизменение. Ок. 100000 слов. - 2-е изд., стереотип. - М.: Рус. яз., 1980. - 880с.
- Дж. фон Нейман Теория самовоспроизводящихся автоматов/ закончено и отредактировано А. Бёрксом. - М.: Мир, 1971. - 384 с.
- З.В.Дударь, Д.Е.Шуклин Семантическая нейронная сеть, как формальный язык описания и обработки смысла текстов на естественном языке // Радиоэлектроника и информатика. Х.: Изд-во ХТУРЭ, 2000. - №. 3. - C. 72-76.
- Представление и использование знаний / Под ред. Х. Уэно, М. Исидзука - М. Мир 1989 - 220с.
- Д.Е.Шуклин Структура семантической нейронной сети извлекающей в реальном времени смысл из текста // Кибернетика и системный анализ. Киев. Изд-во Института кибернетики НАН Украины, 2001. - № 2. С. 43-48.
- З.В.Дударь, Д.Е.Шуклин Реализация нейронов в семантических нейронных сетях // Радиоэлектроника и информатика. Х.: Изд-во ХТУРЭ, 2000. - № 4. С. 89-96.
Источник: (Eidolon) →
Д.Е.Шуклин Структура семантической нейронной сети, реализующей морфологический и синтаксический разбор текста // Кибернетика и системный анализ. Киев. Изд-во Института кибернетики НАН Украины, 2001. - № 5. С. 172-179.
Дополнительно
УДК 519.7
Рецензент: проф., д.т.н. Шабанов-Кушнаренко Ю. П.