Разделы
Счетчики
Могут ли машины мыслить
Turing Alan
Перевод: Долмачев И.
Перевод статьи А. Тьюринга "Могут ли машины мыслить" с дополнениями и пояснениями.
Содержание
- Введение
- I. Игра в имитацию
- II. Критика новой постановки проблемы
- III. Машины, привлекаемые к игре
- IV. Цифровые вычислительные машины
- V. Универсальность цифровых вычислительных машин
Введение
Данный материал был подготовлен И.Долмачевым для сервера vdv.1001.ru и предоставлен им для публикации в нашей газете. В тексте имеются примечания переводчика (они вынесены в сноски) и краткие комментарии И.Долмачева (они выделены из основного текста и помечены: И.А.)
Мы надеемся, что читателям "Информатики" будет очень интересно познакомиться с этой статьей и соотнести ее со статьей А.Н. Колмогорова "Автоматы и жизнь" (см. ).
"Может ли машина мыслить?"-— едва ли не самая знаменитая статья А.Тьюринга. Даже сейчас, спустя почти 50 лет после ее написания, она, вызвавшая в свое время огромное количество как серьезных исследований, так и псевдонаучных спекуляций, нисколько не утеряла своего значения. Статья написана с юмором и иронией ("словно между строк стоят смайлики, по словам Э.Ходжеса, биографа Тьюринга), но за шутливым тоном изложения скрываются одни из самых оригинальных и глубоких идей, высказанных в уходящем веке.
"Игра в имитацию", описанная в этой статье, получила название "теста Тьюринга" (ставшего стандартным теоретическим тестом на "интеллектуальность машины"), который, помимо специалистов по кибернетике, интересовал и некоторых психиатров, усмотревших глубинный психоаналитический смысл в цели игры ("угадывание пола").
Статья была впервые опубликована в научном журнале Mind, v. 59 (1950), pp. 433—460, под названием Computing Machinery and Intelligence и перепечатана в 4-м томе "Мира математики" Аж. Р. Ньюмена {The World of Mathematics. A small library... with commentaries and notes by James R. Newman, Simon & Schuster, NY, v. 4, 1956, pp. 2099-2123), где опубликована под заголовком Can the Machine think? С этого издания был сделан русский перевод, публикуемый здесь по книге:
А.Тьюринг. Может ли машина мыслить? (С приложением статьи Аж. фон Неймана Общая и логическая теория автоматов". Пер.и примечания Ю.В. Данилова). М.: ГИФМЛ, 1960.
I. Игра в имитацию
Я собираюсь рассмотреть вопрос: могут ли машины мыслить. Но для этого нужно сначала определить смысл терминов "машина" и "мыслить". Можно было бы построить эти определения так, чтобы они по возможности лучше отражали обычное употребление этих слов, но такой подход таит в себе некоторую опасность. Дело в том, что, если мы будем выяснять значения слов "машина" и "мыслить", исследуя. как эти слова определяются обычно, нам трудно будет избежать того вывода, что значение этих слов и ответ на, вопрос "могут ли машины мыслить?" следует искать путем статистического обследования наподобие анкетного опроса, проводимого институтом Гэллапа1. Однако это нелепо. Вместо того чтобы пытаться дать такое определение, я заменю Наш вопрос другим, который тесно с ним связан и выражается словами с относительно четким смыслом.
Эта новая форма может быть описана с помощью игрй, которую мы назовем "игрой в имитацию". В этой игре участвуют три человека: мужчина (А), женщина (Б) и кто-нибудь задающий вопросы (С), которым может быть лицо любого пола. Задающий вопросы отделен от двух других участников игры стенами комнаты, в которой он находится. Цель игры для задающего вопросы состоит в том, чтобы определить, кто из двух других участников игры является мужчиной (А), а кто — женщиной (В). Он знает их под обозначениями Х и У и в конце игры говорит либо: "Х есть А и У есть В", либо: "X есть В и У есть А". Ему разрешается задавать вопросы такого, например, рода:
С: "Попрошу Х сообщить мне длину его (или ее) волос".
Допустим теперь, что в действительности Х есть А. В таком случае А и должен давать ответ. Для А цель игры состоит в том, чтобы побудить С прийти к неверному заключению. Поэтому его ответ может быть, например, таким:
"Мои волосы коротко острижены, а самые длинные пряди имеют около девяти дюймов в длину".
Чтобы задающий вопросы не мог определить по голосу, кто из двух других участников игры мужчина, а кто — женщина, ответы на вопросы следовало бы давать в письменном виде, а еще лучше — на пишущей машинке. Идеальным случаем было бы телеграфное сообщение между двумя комнатами, где находятся участники игры. Если же этого сделать нельзя, то ответы и вопросы должен передавать какой-нибудь посредник. Цель игры для третьего игрока — женщины (В) — состоит в том, чтобы помочь задающему вопросы. Для нее, вероятно, лучшая стратегия — давать правдивые ответы. Она также может делать такие замечания, как "Женщина — я, не слушай- -те его!", но этим она ничего не достигнет, так как мужчина тоже может делать подобные замечания.
Поставим теперь вопрос: "Что произойдет, если в этой игре вместо А будет участвовать машина?" Будет ли в этом случае задающий вопросы ошибаться столь же часто, как и в игре, где участниками являются только люди? Эти вопросы и заменят наш первоначальный вопрос "могут ли машины мыслить?".
II. Критика новой постановки проблемы
Подобно тому как мы задаем вопрос: "В чем состоит ответ на проблему в ее новой форме?", можно спросить:
"Заслуживает ли рассмотрения проблема в ее новой постановке?". Этот последний вопрос мы рассмотрим, не откладывая дела в долгий ящик, с тем чтобы в последующем уже не возвращаться к нему.
Новая постановка нашей проблемы имеет то преимущество, что позволяет провести четкое разграничение между физическими и умственными возможностями человека. Ни один инженер или химик не претендует на создание материала, который было бы невозможно отличить от человеческой кожи. Такое изобретение, быть может, когда-нибудь будет сделано. Но даже допустив возможность создания материала, не отличимого от человеческой кожи, мы все же чувствуем, что вряд ли имеет смысл стараться придать "мыслящей машине" большее сходство с человеком, одевая ее в такую искусственную плоть. Форма, которую мы придали проблеме, отражает это обстоятельство в условии, не позволяющем задающему вопросы соприкасаться с другими участниками игры, видеть их или слышать их голоса. Некоторые другие преимущества введенного критерия можно показать, если привести образчики возможных вопросов и ответов. Например:
С: Напишите, пожалуйста, сонет на тему о мосте через реку Форт2.
А: Увольте меня от этого. Мне никогда не приходилось писать стихи.
С: Прибавьте 34 957 к 70 764.
А (молчит около 30 секунд, затем дает ответ): 105 621.
С: Вы играете в шахматы?
А: Да.
С: У меня только король на е8 и других фигур нет. У вас только король на еб и ладья на h1. Как вы сыграете?
А (после 15 секунд молчания): Лh8. Мат.
Нам кажется, что метод вопросов и ответов пригоден для того, чтобы охватить почти любую область человеческой деятельности, какую мы захотим ввести в рассмотрение. Мы не желаем ни ставить в вину машине ее неспособность блистать на конкурсах красоты, ни винить человека в том, что он терпит поражение в состязании с самолетом. условия игры делают эти недостатки несущественными. Отвечающие, если найдут целесообразным, могут хвастать своим обаянием, силой или храбростью, сколько им вздумается, и задающий вопросы не может требовать практических тому доказательств.
Вероятно, нашу игру можно подвергнуть критике на том основании, что в ней преимущества в значительной степени находятся на стороне машины. Если бы человек попытался притвориться машиной, то, очевидно, вид у него был бы весьма жалкий. Он сразу выдал бы себя медлительностью и неточностью при подсчетах. Кроме того, разве машина не может выполнять нечто такое, что следовало бы характеризовать как мышление, но что было бы весьма далеко от того, что делает человек? Это возражение очень веское. Но в ответ на него мы, во всяком случае, можем сказать, что если можно все-таки осуществить такую машину, которая будет удовлетворительно играть в имитацию, то относительно этого возражения особенно беспокоиться не следует.
Можно было бы заметить, что при "игре в имитацию" не исключена возможность того, что простое подражание поведению человека не окажется для машины наилучшей стратегией. Такой случай возможен, но я не думаю, чтобы он привел нас к чему-нибудь существенно новому. Во всяком случае, никто не пытался исследовать теорию нашей игры в этом направлении, и мы будем считать, что наилучшая стратегия для машины состоит в том, чтобы давать ответы, которые в соответствующей обстановке дал бы человек.
III. Машины, привлекаемые к игре
Вопрос, поставленный в разделе I, не станет совершенно точным до тех пор, пока мы не укажем, что именно следует понимать под словом "машина". Разумеется, нам бы хотелось, чтобы в игре можно было применять любой вид инженерной техники. Мы склонны также допустить возможность, что инженер или группа инженеров могут построить машину, которая будет работать, но удовлетворительного описания работы которой они не смогут дать, поскольку метод, которым они пользовались, был в основном экспериментальным [методом проб и ошибок]. Наконец, мы хотели бы исключить из категории машин людей, рожденных обычным образом. Трудно построить определение так, чтобы оно удовлетворяло этим трем условиям. Можно, например, потребовать, чтобы все конструкторы машины были одного пола, в действительности, однако, этого недостаточно, так как, по-видимому, можно вырастить законченный индивидуум из одной-единственной клетки, взятой (например) из кожи человека. Сделать это было бы подвигом биологической техники, заслуживающим самой высокой похвалы, но мы не склонны рассматривать этот случай как "построение мыслящей машины".
Сказанное наводит нас на мысль отказаться от требования, согласно которому в игре следует допускать любой вид техники. Мы еще больше склоняемся к этой мысли в силу того обстоятельства, что наш интерес к "мыслящим машинам" возник благодаря машине особого рода, обычно называемой "электронной вычислительной машиной", или "цифровой вычислительной машиной". Поэтому мы разрешаем принимать участие в нашей игре только цифровым вычислительным машинам.
На первый взгляд это ограничение кажется весьма сильным. Я постараюсь показать, что в действительности дело обстоит не так. Для этого мне придется дать краткий обзор природы и свойств этих вычислительных машин. Можно также "сказать, что отождествление машин с цифровыми вычислительными машинами — равно как и наш критерий "мышления" — должно быть признано совершенно неудовлетворительным, если (вопреки моему убеждению) кажется, что цифровые вычислительные машины не в состоянии хорошо играть в имитацию.
Целый ряд вычислительных машин уже находится в действии, и естественно возникает вопрос: "А почему бы нам, вместо того чтобы сомневаться в правильности наших рассуждений, не поставить эксперимент? Удовлетворить условиям'было бы нетрудно, В качестве задающих вопросы можно было бы использовать много различных людей, и полученные статистические данные показали бы, как часто задающим вопросы удавалось прийти к правильному заключению".
Коротко на этот вопрос можно ответить так: нас интересует не то, будут ли все цифровые вычислительные машины хорошо играть в имитацию, и не то, будут ли хорошо играть в эту игру те вычислительные машины, которыми мы располагаем в настоящее время; вопрос заключается в том, существуют ли воображаемые вычислительные машины, которые могли бы играть хорошо. Но это только краткий ответ. Ниже мы рассмотрим этот вопрос в несколько ином свете.
IV. Цифровые вычислительные машины
То, что мы имеем в виду, говоря о цифровых вычислительных машинах, можно пояснить следующим образом. Предполагается, что эти машины могут выполнять любую операцию, которую мог бы выполнить человек-вычислитель. Мы считаем, что вычислитель придерживается определенных, раз навсегда заданных правил и не имеет права ни в чем отступать от них. Мы можем также считать, что эти правила собраны в книге, которая заменяется другой, когда вычислитель приступает к новой работе. У человека-вычислителя имеется также неограниченный. запас бумаги, на которой он производит вычисления. Кроме того, он может выполнять операции сложения и умножения с помощью арифмометра — это несущественно.
Если данное выше пояснение принять за определение, то возникает угроза того, что наше рассуждение окажется движущимся в замкнутом круге. Чтобы избежать этой опасности, мы приведем перечень тех средств, с помощью которых достигается требуемый эффект. Можно считать, что цифровая вычислительная машина состоит из трех частей:
- запоминающего устройства,
- исполнительного устройства,
- контролирующего устройства.
Запоминающее устройство — это склад информации. Оно соответствует бумаге, имеющейся у человека-вычислителя, независимо от того, является ли эта бумага той, на которой производятся выкладки, или той, на которой напечатана книга правил. Поскольку человек-вычислитель некоторые расчеты проводит в уме, часть запоминающего устройства машины будет соответствовать памяти вычислителя.
Исполнительное устройство — это часть машины, выполняющая разнообразные индивидуальные операции, из которых состоит вычисление. Характер этих операций изменяется от машины к машине. Обычно можно проделывать весьма громоздкие операции, например: "умножить 3 540 675 445 на 7 076 345 687", — однако на некоторых машинах можно выполнять только очень простые операции, вроде таких: "написать 0".
Мы уже упоминали, что имеющаяся у вычислителя "книга правил" заменяется в машине некоторой частью запоминающего устройства, которая в этом случае называется "таблицей команд". Обязанность контролирующего устройства — следить за тем, чтобы эти команды выполнялись безошибочно и в правильном порядке. Контролирующее устройство сконструировано так, что это происходит непременно.
Информация, хранящаяся в запоминающем устройстве, разбивается на небольшие части, которые распределяются по ячейкам памяти. Например, для некоторых машин такая ячейка может состоять из десяти десятичных цифр. Тем ячейкам, в которых хранится различная информация, в некотором определенном порядке приписывают номера. Типичная команда может гласить: .
"Число, хранящееся в ячейке 6809, прибавить к числу, хранящемуся в ячейке 4302, а результат поместить в ту ячейку, где хранилось последнее из чисел".
Нет необходимости говорить о том, что если все это выразить на русском [английском] языке, то машина не выполнит такую команду. Более удобно бьло бы закодировать эту команду в виде, например, числа б 809 430 217. Здесь 17 говорит о том, какую из различных операций, из тех, что можно выполнять с помощью данной машины, следует проделать с числами, хранящимися в указанных ячейках. В данном случае имеется в виду описанная выше операция, т.е. операция "число... прибавить к числу...". Следует заметить, что сама команда занимает 10 цифр и, таким образом, заполняет одну ячейку памяти, что весьма удобно. Обычно контролирующее устройство выбирает необходимые команды в том порядке, в котором они расположены, но иногда могут встречаться и такие команды:
"Теперь выполнить команду, хранящуюся в ячейке 5606, и продолжать оттуда" или же:
"Если ячейка 4505 содержит 0, выполнить команду, содержащуюся в ячейке 6707, в противном случае продолжать по порядку".
Команды этих последних типов очень важны, так как они позволяют повторять снова и снова некоторую последовательность операций до тех пор, пока не будет выполнено определенное условие, причем для повторения данной последовательности операций не приходится прибегать к новым командам. Машина просто выполняет вновь и вновь одни и те же команды. Воспользуемся аналогией из повседневной жизни. Допустим, что мама хочет, чтобы Томми по дороге в школу заходил каждое утро к сапожнику, для того чтобы справиться, не готовы ли ее туфли. Она может каждое утро снова и снова просить его об этом. Но она может также раз и навсегда повесить в прихожей записку, которую Томми будет видеть, уходя в школу, и которая будет напоминать ему о том, чтобы он зашел за туфлями. Когда Томми принесет туфли от сапожника, мама должна разорвать записку.
Читатель должен считать твердо установленным, что цифровые вычислительные машины можно строить на основе тех принципов, о которых мы рассказали выше, и что их действительно строят, придерживаясь этих принципов. Ему должно быть ясно, что цифровые вычислительные машины могут в действительности весьма точно подражать действиям человека-вычислителя.
Разумеется, описанная нами книга правил, которой пользуется вычислитель, является всего лишь удобной фикцией. На самом деле настоящие вычислители помнят, что они должны делать. Если мы хотим построить машину, подражающую действиям человека-вычислителя при выполнении некоторой сложной операции, то следует спросить последнего, как он выполняет эту операцию, и ответ представить в виде таблицы команд.
Составление таблицы команд обычно называют "программированием". "Запрограммировать выполнение машинной операции А" — значит ввести в машину подходящую таблицу команд, следуя которым машина может выполнить операцию А.
Интересной разновидностью цифровых вычислительных машин являются "цифровые вычислительные машины со случайным элементом". Такие машины имеют команды, содержащие бросание игральной кости или какой-нибудь эквивалентный электронный процесс. Одной из таких команд может быть, например, следующая: "бросить кость и полученное при бросании число поместить в ячейку 1000". Иногда говорят, что такие машины обладают свободой выбора (хотя лично я не стал бы употреблять такое выражение) . Установить наличие "случайного элемента" в машине путем наблюдений за ее действием обычно оказывается невозможным, так как если сделать, например, выбор команды зависимым от последовательности цифр в десятичном разложении числа р, то результат получится совершенно аналогичный.
Все существующие в действительности цифровые вычислительные машины обладают лишь конечной памятью. Однако теоретически нетрудно представить себе машину с неограниченной памятью. Разумеется, в любой данный момент времени возможно использование только конечной части запоминающего устройства. Точно так же запоминающее устройство, которое можно физически осуществить, всегда имеет конечные размеры, но мы можем представлять дело так, что по мере надобности к нему пристраиваются все новые и новые части. Такие вычислительные машины представляют особый теоретический интерес, и впредь мы будем их называть машинами с бесконечной емкостью памяти.
Сама идея цифровой вычислительной машины отнюдь не является новой. Чарлз Бэббидж3, занимавший с 1828-го по 1839 г. Люкасовскую кафедру по математике в Кембридже4, разработал проект вычислительного устройства, названного им "Аналитической машиной"; создание ее, однако, так и не удалось завершить. Хотя у Бэббиджа были все основные идеи, существенные для создания такого механизма, его машина не имела перспектив. Скорость вычислений, которую позволила бы достичь машина Бэббиджа, оказалась бы, разумеется, выше скорости, достигаемой человеком, однако она была бы почти в 100 раз меньше, чем у той вычислительной машины, которая в настоящее время работает в Манчестере5 и которая является одной из самых медленных современных машин. Запоминающее устройство в машине Бэббиджа было задумано как чисто механическое, с использованием карт и зубчатых колес.
То, что Аналитическая машина Бэббиджа была задумана как чисто механический аппарат, помогает нам избавиться от одного предрассудка. Часто придают значение тому обстоятельству, что современные цифровые машины являются электрическими устройствами и что нервную систему человека в некотором смысле можно отождествить с электрическим устройством. Но, поскольку машина Бэббиджа не была электрическим аппаратом и поскольку в известном смысле все цифровые вычислительные машины эквивалентны, становится ясно, что использование электричества в этом случае не может иметь теоретического значения. Естественно, что там, где требуется быстрая передача сигналов, обычно появляется электричество, поэтому неудивительно, что мы встречаем его в обоих указанных случаях. Для нервной системы химические явления играют по крайней мере столь же важную роль, что и электрические. В некоторых же вычислительных машинах запоминающее устройство в основном акустическое. Отсюда ясно, что сходство между нервной системой и цифровыми вычислительными машинами, состоящее в том, что в обоих случаях используется электричество, сводится лишь к весьма поверхностной аналогии. Если мы действительно хотим открыть глубокие связи, нам скорее следует искать сходство в математических моделях функционирования нервной системы и цифровых вычислительных машин.
V. Универсальность цифровых вычислительных машин
Рассмотренные в предыдущем разделе цифровые вычислительные машины можно отнести к классу "машин с дискретными состояниями". Так называются машины, работа которых складывается из совершающихся последовательно одна за другой резких смен их состояния. Состояния, о которых идет речь, достаточно отличаются друг от друга, поэтому можно пренебречь возможностью принять по ошибке одно из них за другое. Строго говоря, таких машин не существует. В действительности всякое движение непрерывно. Однако имеется много видов машин, которые удобно считать машинами с дискретными состояниями.
Например, если рассматривать выключатели осветительной сети, то удобно считать, отвлекаясь от действительного положения дела, что каждый выключатель может быть либо включён, либо выключен. То, что выключатель фактически имеет также и промежуточные состояния, несущественно для наших целей, и мы можем об этом забыть. Приведу пример машины с дискретными состояниями. Рассмотрим колесико, способное через каждую секунду совершать скачкообразный поворот (щелчок) на 120°, но которое можно застопоривать с помощью рычажка, управляемого извне. Пусть, кроме того, в момент, когда колесико принимает какое-нибудь определенное положение (одно из трех возможных для него), загорается лампочка. В абстрактном виде эта машина выглядит так. Внутреннее состояние машины (которое задается положением колесика) может быть q1, q2 или q3. На вход машины подается либо сигнал i0 либо сигнал i1 (положения рычажка). Внутреннее состояние в любой момент определено предыдущим состоянием и сигналом на входе согласно следующей таблице:
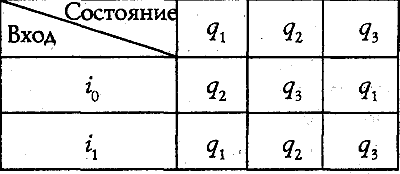
Статья не закончена. Полный вариант см. в источнике.
1 - Институт Гэллапа — Американский институт общественного мнения American Institute of Public Opinion. Основан Дж. Гэллапом (GeorgeGallup) в l935r.
2 - Мост через реку Форт — известный мост консольно-арочного типа, в два пролета, перекрывающий реку форт (Шотландия) при впадении ее в залив Ферт-оф-Форт. Сооружен в 1882—1889 гг. и в течение 28 лет держал мировой рекорд длины пролетов (длина каждого пролета — свыше 518 м, длина моста — около 1626 м).
3 - Чарлз Бэббидж (Charles Babbage) (1792—1871) —английский ученый, работавший в области математики, вычислительной техники и механики. Выступил инициатором применения механических устройств для вычисления и печатания математических таблиц. В 1812 г. у Бэббиджа возникла идея разностной вычислительной машины (Difference Engine). Строительство этой машины, которая должна была вычислять любую функцию, заданную ее первыми пятью разностями, началось в 1823 г. на средства английского правительства, однако в 1833 г. работа была прекращена главным образом в связи с финансовыми затруднениями. К этому времени у Бэббиджа возник проект другой, более совершенной машины. Эта машина, которую Бэббидж назвал "Аналитической машиной" (Analitical Engine), должна была проводить вычислительный процесс, заданный любыми математическими формулами. Бэббидж весь отдался конструированию своей новой машины, однако к моменту его смерти она так и не была закончена. Сын Бэббиджа завершил строительство части машины и провел успешные опыты по применению ее для вычислений некоторого рода.
4 - Аюкасовская кафедра в Тринити-колледже основана в 1663 г. на средства, пожертвованные Генри Люкасом. Первым люкасовским профессором был учитель Ньютона Барроу, вторым — сам Ньютон. Получение этой кафедры, сохранившейся до нашего времени, считалось всегда большой честью.
5 - Манчестерская машина была построена в Манчестерском университете в конце 40-х годов. Конструирование машины происходило под руководством Вильямса (Р.С. Williams) и Килберна (T.Kilburn). В разработке и отладке машины принимал участие Тьюринг, который с этой целью в 1948 г. был приглашен в Манчестерский университет. Тьюринг занимался математическими вопросами, связанными с Манчестерской машиной, и особенно вопросами программирования.
6 - Единицы, о которых говорит здесь Тьюринг, получили название "битов" (bits) По причинам, связанным с компьютеростроением, основной единицей измерения емкости машинной памяти стали "байты" (bytes) Ответ на вопрос "Сколько бит [ов] в байте?" с исторической точки зрения довольно темен (байт — емкость памяти, предназначенной для размещения одного символа), но стандартом de facto является соглашение 1 байт = 8 бит. Более крупными производными единицами являются килобайт (Кб) = 210 = 1024 байт, мегабайт (Мб) = 210 = 1024 Кб Сейчас уже никого не удивляют гигабайты (Г6) и даже терабайты (Тб) Для более точного выражения единиц памяти (например, в синтезаторостроении) употребляются также единицы килобит (Кбит), мегабит (Мбит) и т.д.
7 - Возможно, эта точка зрения еретична. Св. Фома Аквинский (Summa Theologica; его взгляд излагается в книге Bertrand Russell, History of Western Philosophy, Simon and Schuster, New York, 1946, p. 458 [русское издание, например: Б.Рассел. История западной философиии. Новосибирск, изд-воНГУ, 1994] ) утверждает, что Бог не может лишить человека души, но что это не является реальным ограничением его всемогущества, а есть всего лишь результат того факта, что человеческие души бессмертны и, следовательно, неуничтожимы.
 Скачать (html) (41,1 Kb)
Скачать (html) (41,1 Kb)
Источники: 1. (Информатика)
2. (Компьютерный диалог)
3.
4. Алан М. Тьюринг Может ли машина мыслить? - М.: "Государственное издательство физико-математической литературы", 1960 - 112с.